Chủ đề consecutive integer: Khám phá thế giới kỳ diệu của "Consecutive Integer" qua bài viết này, nơi chúng ta sẽ đưa bạn đi từ những định nghĩa cơ bản đến các ứng dụng sâu sắc và thú vị trong toán học cũng như cuộc sống hàng ngày. Hãy cùng chúng tôi mở rộng kiến thức và khám phá những bí mật đằng sau các chuỗi số liên tiếp, từ việc giải các bài toán phức tạp đến việc áp dụng chúng trong các tình huống thực tế.
Mục lục
- Định Nghĩa
- Công Thức
- Tính Chất
- Số Nguyên Liên Tiếp Lẻ và Chẵn
- Có bao nhiêu cặp số nguyên liên tiếp khi nhân với nhau thì ra kết quả như công thức N! = N×(N – 1)×(N – 2)×…×3×2×1?
- YOUTUBE: Giải bài toán số nguyên liên tiếp bằng phương pháp đại số | Phương trình tuyến tính | Đại số I | Khan Academy
- Định Nghĩa và Giới Thiệu
- Công Thức và Cách Tính
- Ví dụ Minh Họa
- Tính Chất của Số Nguyên Liên Tiếp
- Ứng Dụng trong Toán Học và Cuộc Sống
- Cách Giải Bài Toán Sử Dụng Số Nguyên Liên Tiếp
- Thách Thức và Bài Toán Mở
- FAQ - Câu Hỏi Thường Gặp
- Tài Nguyên và Công Cụ Hữu Ích
Định Nghĩa
Số nguyên liên tiếp có thể được hiểu là một dãy số nguyên mà trong đó, mỗi số tiếp theo lớn hơn số trước đó một đơn vị.
Ví dụ:
- -2, -1, 0, 1, 2 là một chuỗi số nguyên liên tiếp.
- 7, 8, 9 cũng là một chuỗi số nguyên liên tiếp.

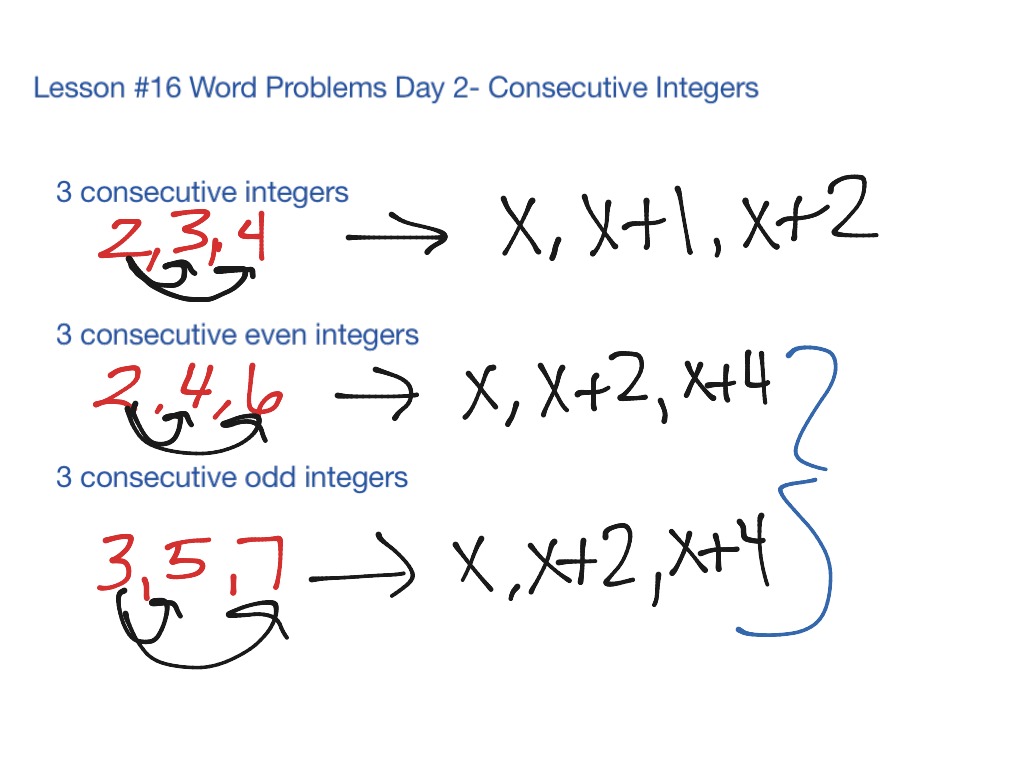
Công Thức
Nếu x là một số nguyên, thì x + 1, x + 2, ... là các số nguyên liên tiếp tiếp theo.
Tính Chất
- Sự chênh lệch giữa mỗi cặp số nguyên liên tiếp là không đổi và bằng 1.
- Trong một chuỗi số nguyên liên tiếp, trung bình cộng và trung vị là bằng nhau.
- Hệ số chung lớn nhất (HCF) của hai số nguyên liên tiếp luôn là 1.

Số Nguyên Liên Tiếp Lẻ và Chẵn
Số nguyên liên tiếp cũng có thể được phân loại thành số nguyên liên tiếp lẻ hoặc chẵn, với sự chênh lệch là 2 giữa mỗi số trong chuỗi.
| Loại | Ví dụ |
| Số Nguyên Liên Tiếp Lẻ | 1, 3, 5, 7 |
| Số Nguyên Liên Tiếp Chẵn | 2, 4, 6, 8 |
Có bao nhiêu cặp số nguyên liên tiếp khi nhân với nhau thì ra kết quả như công thức N! = N×(N – 1)×(N – 2)×…×3×2×1?
Để tìm số lượng cặp số nguyên liên tiếp thỏa mãn công thức N! = N×(N – 1)×(N – 2)×…×3×2×1, ta cần phân tích công thức này theo từng bước:
- Ta biết rằng N! = N×(N-1)×(N-2)×...×3×2×1
- Thay N! = N×(N-1)×(N-2)×...×3×2×1 vào công thức đã cho, ta được:
- N×(N-1)×(N-2)×...×3×2×1 = N×(N-1)×(N-2)×...×3×2×1
- Do đó, các số nguyên liên tiếp cần có tính chất \"Nếu nhân lần lượt các số này, ta sẽ được kết quả như công thức N! = N×(N – 1)×(N – 2)×…×3×2×1\"
- Các số nguyên liên tiếp là 3 và 2
Vậy, chỉ có 2 cặp số nguyên liên tiếp là 3 và 2 thỏa mãn điều kiện đã cho.
Giải bài toán số nguyên liên tiếp bằng phương pháp đại số | Phương trình tuyến tính | Đại số I | Khan Academy
\"Khám phá bí mật của số nguyên liên tiếp và cách tính tổng ba số liên tiếp. Điều gì sẽ xảy ra khi bạn kết hợp chúng? Hãy trải nghiệm ngay trên Youtube!\"
Cách tìm ba số nguyên liên tiếp có tổng đã cho
Write an equation to find 3 consecutive integers that equal 159. Visit https://maisonetmath.com for more tutorials, online quizzes ...
Định Nghĩa và Giới Thiệu
Số nguyên liên tiếp là những số nguyên theo sau nhau mà không có bất kỳ khoảng trống nào giữa chúng, với mỗi số chỉ cách nhau một đơn vị. Chúng tạo thành một chuỗi số mà trong đó, mỗi số tiếp theo là kết quả của việc cộng thêm một vào số trước đó. Số nguyên liên tiếp có thể bao gồm cả số nguyên âm và dương, tạo ra một chuỗi không giới hạn các số.
- Chuỗi số nguyên liên tiếp: 1, 2, 3, 4, ...
- Chuỗi số nguyên liên tiếp âm: -3, -2, -1, 0, 1, ...
Trong toán học, chuỗi số nguyên liên tiếp được sử dụng rộng rãi trong các bài toán, từ đơn giản đến phức tạp, giúp giải thích và hiểu biết sâu sắc về cấu trúc và tính chất của số nguyên.
| Thuật ngữ | Ý nghĩa |
| Số nguyên liên tiếp | Các số nguyên xếp liền kề nhau không có khoảng cách |
| Chuỗi số nguyên dương liên tiếp | Chuỗi số bắt đầu từ 1 và tăng dần |
| Chuỗi số nguyên âm liên tiếp | Chuỗi số bắt đầu từ một số âm và giảm dần |
Hiểu rõ về số nguyên liên tiếp không chỉ giúp giải các bài toán một cách chính xác mà còn mở ra cánh cửa khám phá thế giới toán học phong phú và đa dạng.
Công Thức và Cách Tính
Để xác định chuỗi số nguyên liên tiếp, chúng ta sử dụng công thức đơn giản nhưng mạnh mẽ. Nếu x là số nguyên đầu tiên trong chuỗi, số nguyên liên tiếp tiếp theo sẽ là x + 1, kế tiếp là x + 2, và cứ thế tiếp tục. Công thức này giúp xác định một chuỗi số nguyên liên tiếp mà không có giới hạn.
- Nếu x = 1, chuỗi số nguyên liên tiếp sẽ là: 1, 2, 3, 4, ...
- Chuỗi số nguyên liên tiếp âm bắt đầu từ x = -3 sẽ là: -3, -2, -1, 0, 1, ...
Đối với số nguyên liên tiếp chẵn hoặc lẻ, chúng ta cũng có công thức đặc biệt:
- Số nguyên liên tiếp chẵn: Nếu x là số chẵn, chuỗi số nguyên liên tiếp chẵn sẽ là x, x + 2, x + 4, ...
- Số nguyên liên tiếp lẻ: Nếu n biểu diễn một số nguyên, chuỗi số nguyên liên tiếp lẻ có thể được biểu diễn qua công thức 2n + 1, 2n + 3, 2n + 5, ...
Việc áp dụng các công thức này không chỉ giúp giải các bài toán liên quan một cách dễ dàng mà còn mở rộng hiểu biết về cấu trúc và tính chất của các số nguyên trong toán học.
Ví dụ Minh Họa
Để hiểu rõ hơn về cách sử dụng và tính toán số nguyên liên tiếp, hãy xem xét một số ví dụ minh họa sau:
- Ví dụ 1: Tìm ba số nguyên liên tiếp có tổng là 138. Giả sử số đầu tiên là n, ba số sẽ là n, n+1, và n+2. Đặt tổng ba số này bằng 138, ta có phương trình n + (n+1) + (n+2) = 138. Giải phương trình này để tìm n.
- Ví dụ 2: Tìm hai số nguyên liên tiếp có tích là 156. Sử dụng kiến thức về số nguyên liên tiếp và tính chất của chúng, ta biết rằng một trong hai số phải nằm giữa hai bình phương liên tiếp. Trong trường hợp này, số đó là 12 và 13, vì 12 * 12 = 144 và 13 * 13 = 169, và 12 * 13 = 156.
- Ví dụ 3: Xác định ba số nguyên liên tiếp lẻ theo sau số -11. Bắt đầu từ -11, ba số nguyên liên tiếp lẻ tiếp theo sẽ là -9, -7, và -5.
Những ví dụ này chỉ ra cách áp dụng công thức và hiểu biết về số nguyên liên tiếp vào giải quyết các vấn đề toán học cụ thể, từ đơn giản đến phức tạp.

Tính Chất của Số Nguyên Liên Tiếp
Số nguyên liên tiếp có những tính chất đặc biệt mà khi hiểu rõ, chúng ta có thể ứng dụng vào giải các bài toán toán học một cách hiệu quả. Dưới đây là một số tính chất nổi bật của số nguyên liên tiếp:
- Sự chênh lệch giữa hai số nguyên liên tiếp luôn là một.
- Trong bất kỳ dãy số nguyên liên tiếp nào, trung bình cộng và trung vị của dãy đó bằng nhau.
- Trong dãy số nguyên liên tiếp, luôn có một số chia hết cho nếu dãy đó gồm n số liên tiếp.
- Mọi cặp số nguyên liên tiếp lẻ hoặc chẵn đều có sự chênh lệch là 2.
Các tính chất này không chỉ giúp chúng ta hiểu biết sâu sắc hơn về cấu trúc của số nguyên trong toán học mà còn là nền tảng quan trọng trong việc giải quyết các vấn đề toán học phức tạp, từ đơn giản như tìm số tiếp theo trong chuỗi đến phức tạp như chứng minh các định lý liên quan.
Ứng Dụng trong Toán Học và Cuộc Sống
Số nguyên liên tiếp không chỉ là một khái niệm toán học cơ bản mà còn có ứng dụng rộng rãi trong cuộc sống hàng ngày và các lĩnh vực khoa học khác. Dưới đây là một số ứng dụng tiêu biểu:
- Toán học: Giải các bài toán đại số, bao gồm tìm số nguyên liên tiếp dựa trên tổng, hiệu, hoặc tích của chúng. Số nguyên liên tiếp được sử dụng để chứng minh các định lý toán học và giải các phương trình.
- Khoa học máy tính: Trong lập trình, các dãy số nguyên liên tiếp thường được sử dụng để duyệt qua các phần tử của mảng hoặc để xử lý lặp lại.
- Quản lý dự án: Số nguyên liên tiếp có thể được sử dụng trong quản lý dự án để xác định thứ tự ưu tiên công việc hoặc lên kế hoạch thời gian.
- Giáo dục: Giáo viên sử dụng số nguyên liên tiếp như một công cụ giảng dạy để giúp học sinh hiểu về mối quan hệ giữa các số và cách chúng kết nối với nhau.
- Đời sống hàng ngày: Số nguyên liên tiếp cũng xuất hiện trong việc đánh số trang sách, số nhà, hoặc sắp xếp chỗ ngồi theo thứ tự tại các sự kiện.
Qua đó, có thể thấy số nguyên liên tiếp không chỉ quan trọng trong toán học mà còn ảnh hưởng đến nhiều khía cạnh khác của cuộc sống và khoa học.

Cách Giải Bài Toán Sử Dụng Số Nguyên Liên Tiếp
Giải bài toán số nguyên liên tiếp đòi hỏi phương pháp tiếp cận hệ thống và một số bước cơ bản như sau:
- Xác định yêu cầu của bài toán: Đầu tiên, xác định bài toán yêu cầu tìm số nguyên liên tiếp nào - có phải tất cả số nguyên, chỉ số nguyên chẵn, hay chỉ số nguyên lẻ.
- Chọn biến số đại diện: Gán biến (thường là x) cho số nguyên đầu tiên trong chuỗi. Số nguyên liên tiếp tiếp theo sẽ được biểu diễn qua x + 1, x + 2, và tiếp tục tùy thuộc vào yêu cầu của bài toán.
- Lập phương trình: Dựa vào thông tin được cung cấp trong đề bài, lập phương trình sử dụng các biến đã xác định. Phương trình này có thể liên quan đến tổng, hiệu, hoặc tích của các số nguyên liên tiếp.
- Giải phương trình: Sử dụng kỹ thuật đại số để giải phương trình và tìm giá trị của biến.
- Kiểm tra kết quả: Cuối cùng, hãy kiểm tra xem kết quả có thỏa mãn điều kiện của bài toán hay không.
Ví dụ, nếu bài toán yêu cầu tìm ba số nguyên liên tiếp có tổng là 9, ta có thể gán x cho số đầu tiên, từ đó ba số sẽ là x, x + 1, và x + 2. Lập phương trình x + (x + 1) + (x + 2) = 9, giải phương trình để tìm x, và từ đó tìm được ba số nguyên liên tiếp cần tìm.
Thách Thức và Bài Toán Mở
Mặc dù số nguyên liên tiếp là một khái niệm cơ bản trong toán học, nhưng nó vẫn mở ra những thách thức và bài toán mở khi áp dụng vào các vấn đề phức tạp hơn:
- Xác định mẫu số chung: Tìm hiểu về cách xác định mẫu số chung của các dãy số nguyên liên tiếp dài và phức tạp là một thách thức, đặc biệt khi áp dụng trong lý thuyết số và phân tích số học.
- Giải các bài toán phân tích: Sử dụng số nguyên liên tiếp trong việc giải các bài toán phân tích và chứng minh các định lý liên quan đến cấu trúc của số nguyên, đặc biệt là trong các dãy số đặc biệt.
- Ứng dụng trong lập trình: Xác định cách sử dụng hiệu quả các chuỗi số nguyên liên tiếp trong các thuật toán và cấu trúc dữ liệu là một lĩnh vực mở cho các nhà khoa học máy tính.
- Ứng dụng trong các bài toán thực tế: Tìm cách áp dụng số nguyên liên tiếp vào giải quyết các vấn đề thực tế trong khoa học, kỹ thuật và các lĩnh vực khác đòi hỏi sự sáng tạo và đổi mới.
Những thách thức và bài toán mở này không chỉ thúc đẩy sự hiểu biết sâu sắc hơn về toán học mà còn tạo cơ hội cho các nhà nghiên cứu phát triển các giải pháp mới, mở rộng kiến thức và ứng dụng của số nguyên liên tiếp trong nhiều lĩnh vực.

FAQ - Câu Hỏi Thường Gặp
- Số nguyên liên tiếp là gì? Số nguyên liên tiếp là những số nguyên xếp liền kề nhau mà không có khoảng cách, với mỗi số hơn kém nhau một đơn vị.
- Làm thế nào để tìm số nguyên liên tiếp? Để tìm số nguyên liên tiếp, xác định số nguyên đầu tiên và sử dụng công thức x, x+1, x+2, ..., nơi x là số nguyên đầu tiên.
- Số nguyên liên tiếp chẵn/lẻ có tính chất gì đặc biệt? Số nguyên liên tiếp chẵn hoặc lẻ có sự chênh lệch là 2 giữa mỗi số. Ví dụ, nếu x là số chẵn, chuỗi số nguyên liên tiếp chẵn sẽ là x, x+2, x+4, và nếu n là số lẻ, chuỗi số nguyên liên tiếp lẻ sẽ là n, n+2, n+4.
- Có bao nhiêu số nguyên liên tiếp tạo nên một dãy nhất định? Số lượng số nguyên liên tiếp tạo nên một dãy phụ thuộc vào điều kiện cụ thể của bài toán. Không có giới hạn cố định cho số lượng số nguyên liên tiếp trong một dãy.
- Cách giải bài toán số nguyên liên tiếp? Để giải bài toán số nguyên liên tiếp, xác định số nguyên đầu tiên của dãy, lập phương trình dựa trên yêu cầu của bài toán, và sử dụng kỹ thuật đại số để giải phương trình và tìm ra dãy số nguyên liên tiếp cần tìm.
Tài Nguyên và Công Cụ Hữu Ích
Để giải các bài toán liên quan đến số nguyên liên tiếp, có nhiều tài nguyên và công cụ sẵn có trên mạng giúp việc học và giải bài trở nên dễ dàng hơn:
- Khan Academy cung cấp các video giảng dạy chi tiết về cách giải quyết các bài toán sử dụng số nguyên liên tiếp, bao gồm cả số nguyên liên tiếp lẻ và chẵn.
- Omni Calculator cung cấp một công cụ tính toán cho phép giải quyết các bài toán liên quan đến tổng hoặc tích của các số nguyên liên tiếp, với khả năng điều chỉnh để tìm kiếm số nguyên liên tiếp bất kỳ, chẵn hoặc lẻ.
- Krista King Math cung cấp các khóa học từ Pre-Algebra đến Calculus 3, bao gồm cả các bài giảng về cách giải các bài toán liên quan đến số nguyên liên tiếp, cùng với nhiều tài nguyên học tập khác.
Những tài nguyên này không chỉ giúp bạn hiểu rõ về số nguyên liên tiếp và cách giải các bài toán liên quan mà còn cung cấp công cụ hữu ích để thực hành và áp dụng kiến thức đã học.
Khám phá thế giới của số nguyên liên tiếp không chỉ mở ra cánh cửa kiến thức toán học vô tận mà còn giúp bạn áp dụng vào giải quyết các vấn đề thực tế một cách sáng tạo. Hãy bắt đầu hành trình khám phá ngay hôm nay!