Số Nguyên Liên Tiếp: Khám Phá Bí Mật Toán Học Qua Các Con Số

Số nguyên liên tiếp là những số theo sau nhau một cách liên tục. Ví dụ, một dãy số tự nhiên được coi là các số nguyên liên tiếp. Trong toán học, "liên tiếp" có nghĩa là một chuỗi không bị gián đoạn hoặc theo sau một cách liên tục, nên các số nguyên liên tiếp theo một chuỗi mà mỗi số tiếp theo lớn hơn số trước đó một đơn vị.

Công Thức

Đối với các số nguyên liên tiếp, chúng ta có thể biểu diễn chúng dưới dạng n, n+1, n+2, ..., trong đó n là một số nguyên.

Tính Chất

• Mỗi số nguyên liên tiếp trong chuỗi có khoảng cách là 1 đơn vị.
• Bất kỳ hai số nguyên lẻ hoặc chẵn liên tiếp nào đều có sự khác biệt là 2.
• Trong một chuỗi gồm n số nguyên liên tiếp, sẽ có đúng một số chia hết cho n.
• Sản phẩm của ba số nguyên liên tiếp (không kể số 0) luôn chia hết cho 6.

Ví dụ một chuỗi số nguyên liên tiếp là 1, 2, 3, 4. Một ví dụ khác là 7, 8, 9. Nói chung, một chuỗi số nguyên liên tiếp là một chuỗi số mà mỗi thuật ngữ lớn hơn thuật ngữ trước đó một đơn vị.

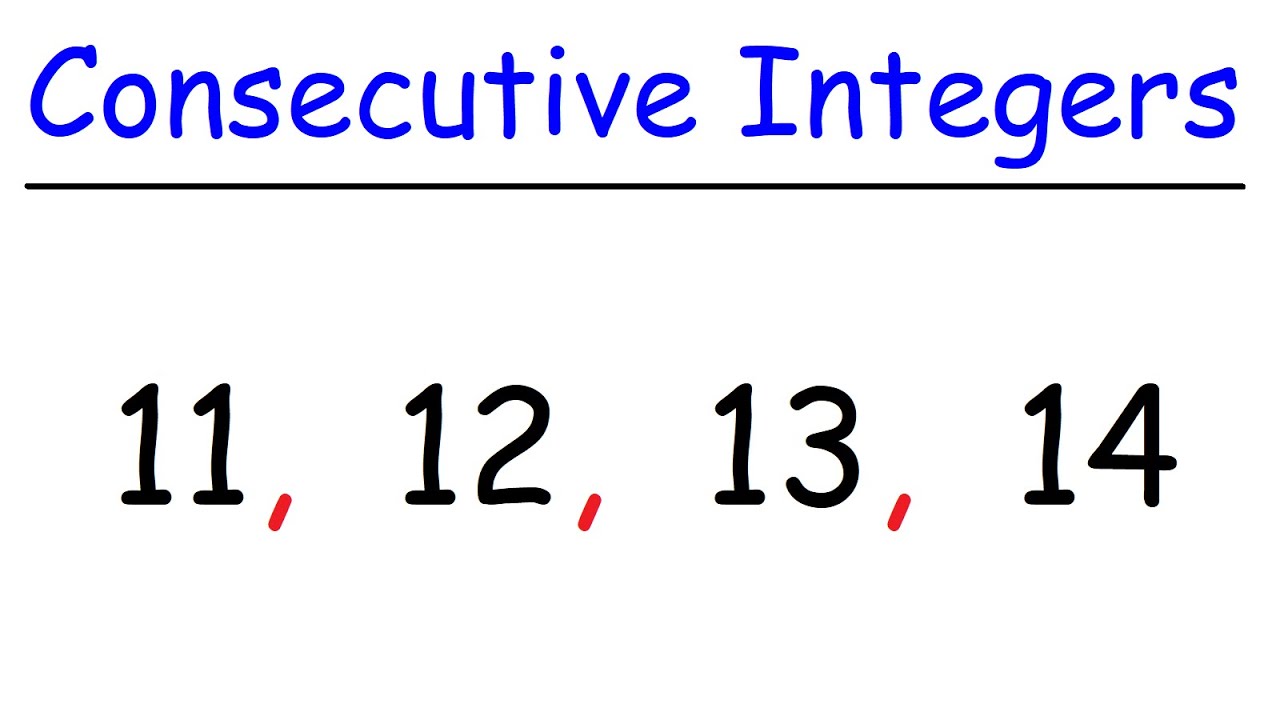
Số nguyên liên tiếp có thể bắt đầu bằng bất kỳ số nguyên toàn vẹn nào, không chỉ là số 1. Ví dụ, cặp số 42 và 43 là số nguyên liên tiếp. Có cả số nguyên liên tiếp lẻ hoặc chẵn, bắt đầu từ một số nguyên lẻ hoặc chẵn và tăng lên hoặc giảm xuống theo bước nhảy là 2.

Các thông tin về tổ hợp số nguyên liên tiếp mà bạn có thể tìm thấy trên Google bao gồm:

• Một ví dụ về ba số nguyên dương liên tiếp, trong đó tích của hai số cuối cùng lớn hơn 80.
• Cách tìm các số nguyên dương liên tiếp từ 1 đến 999 sao cho tích của sáu số đó kết thúc bằng một số cụ thể.
• Ví dụ về việc tìm số nguyên trong một dãy số liên tiếp dựa trên thông tin về số lượng số nguyên liên tiếp và sự liên quan giữa chúng.

Số nguyên liên tiếp là những số nguyên được sắp xếp theo thứ tự tăng dần mà khoảng cách giữa mỗi số liên tiếp là đúng một đơn vị. Sự hiểu biết về các số nguyên liên tiếp có vai trò quan trọng trong nhiều lĩnh vực toán học, từ giải quyết bài toán đại số đến việc phân tích mô hình số học.

• Số nguyên liên tiếp thường được biểu diễn dưới dạng n, n+1, n+2, ..., nơi n là một số nguyên bất kỳ.
• Chúng có thể được sử dụng để mô tả và giải quyết các bài toán liên quan đến tổng số, sản phẩm của số, hoặc các vấn đề phân chia.
• Phân biệt được giữa số nguyên liên tiếp chung và số nguyên liên tiếp chẵn hoặc lẻ là quan trọng, bởi vì chúng tuân theo quy tắc riêng và có các tính chất đặc biệt.

Khái niệm về số nguyên liên tiếp mở rộng sự hiểu biết và khả năng áp dụng toán học vào thực tiễn, giúp làm sáng tỏ các mô hình và cấu trúc số học phức tạp trong cuộc sống hàng ngày và trong nghiên cứu khoa học.

Số nguyên liên tiếp là những số nguyên mà mỗi số tiếp theo là số kế nhiệm của số trước đó, tức là chúng tăng dần lên một đơn vị. Ví dụ, các số -3, -2, -1, 0, 1, 2 là một chuỗi số nguyên liên tiếp.

Để biểu diễn một chuỗi số nguyên liên tiếp trong toán học, ta thường sử dụng biểu thức n, n+1, n+2, ..., n+k, với n là số nguyên bắt đầu và k là số nguyên dương chỉ số lượng phần tử trong chuỗi trừ một.

• Số nguyên liên tiếp dương: Ví dụ, 1, 2, 3, ...
• Số nguyên liên tiếp âm: Ví dụ, -3, -2, -1, ...

Công thức cơ bản: Để tìm số nguyên kế tiếp của một số nguyên n, ta chỉ cần cộng thêm 1 vào số nguyên đó (n+1). Tương tự, để tìm số nguyên trước một số nguyên n, ta trừ đi 1 (n-1).

1. Đối với số nguyên liên tiếp chẵn hoặc lẻ, chúng ta thêm hoặc bớt 2 thay vì 1 để giữ tính chẵn hoặc lẻ của số.
2. Trong một dãy số nguyên liên tiếp, trung bình cộng và trung vị đều bằng nhau và bằng số nằm chính giữa dãy (nếu dãy có số lượng phần tử là lẻ) hoặc bằng trung bình cộng của hai số nằm giữa (nếu dãy có số lượng phần tử là chẵn).

Ví dụ: Tìm ba số nguyên liên tiếp có tổng là 51. Giả sử số đầu tiên là x, số thứ hai là x+1, và số thứ ba là x+2. Ta có phương trình: x + (x+1) + (x+2) = 51. Giải phương trình này, ta được x = 16. Vậy ba số cần tìm là 16, 17, và 18.

Các số nguyên liên tiếp có nhiều tính chất thú vị và ứng dụng quan trọng trong toán học. Dưới đây là một số tính chất và ví dụ minh họa cụ thể:

• Mỗi số nguyên trong một dãy số nguyên liên tiếp khác biệt nhau bởi một đơn vị.
• Số lượng chẵn và số lượng lẻ trong một dãy số nguyên liên tiếp có thể thay đổi tùy thuộc vào điểm bắt đầu của dãy.
• Tích của ba số nguyên liên tiếp bất kỳ luôn chia hết cho 6.
• Mỗi dãy gồm n số nguyên liên tiếp luôn có đúng một số chia hết cho n.

Ứng dụng: Số nguyên liên tiếp được sử dụng rộng rãi trong giải quyết các bài toán toán học, từ việc tìm kiếm các số cụ thể trong một dãy cho đến giải các bài toán liên quan đến tổng và tích của các số nguyên liên tiếp.

1. Giải bài toán tìm số: Ví dụ, tìm ba số nguyên liên tiếp có tổng là một số cụ thể.
2. Ứng dụng trong các bài toán liên quan đến các tính chất đặc biệt của số nguyên, như bài toán chia hết.

Ví dụ minh họa: Tìm ba số nguyên liên tiếp có tổng bằng 51. Giải pháp là chia tổng cho 3 và tìm số nguyên ở giữa, sau đó tìm hai số còn lại dựa trên số này.

Số nguyên liên tiếp có nhiều ví dụ minh họa giúp chúng ta hiểu rõ hơn về khái niệm này trong toán học. Dưới đây là một số ví dụ đặc biệt:

1. Tìm ba số nguyên liên tiếp có tổng là 51. Giả sử số đầu tiên là x, ta có x + (x + 1) + (x + 2) = 51. Giải phương trình, ta được x = 16. Vậy ba số cần tìm là 16, 17, và 18.
2. Tìm bốn số nguyên liên tiếp lẻ có tổng là 64. Gọi số đầu tiên là x, các số tiếp theo sẽ là x + 2, x + 4, và x + 6. Tổng của chúng là 64, và từ đó ta tìm được x = 13. Vậy các số cần tìm là 13, 15, 17, và 19.
3. Tìm ba số nguyên liên tiếp có tổng là 78. Sử dụng cùng phương pháp, ta tìm được ba số là 25, 26, và 27.
4. Tìm ba số nguyên liên tiếp lẻ sau số -11. Với x = -11, ba số liên tiếp lẻ tiếp theo sẽ là -9, -7, và -5.

Các ví dụ trên minh họa cách áp dụng công thức và logic toán học để giải quyết các bài toán liên quan đến số nguyên liên tiếp, từ đơn giản đến phức tạp.

Để tìm chuỗi số nguyên liên tiếp thỏa mãn một điều kiện cho trước, chúng ta có thể áp dụng một số phương pháp dựa trên đặc điểm của chuỗi số nguyên liên tiếp:

1. Xác định công thức: Một chuỗi số nguyên liên tiếp có thể được biểu diễn dưới dạng n, n+1, n+2, v.v. Tùy vào yêu cầu của bài toán, công thức này có thể thay đổi để thỏa mãn các điều kiện như tổng, tích, hay chênh lệch giữa các số.
2. Sử dụng phương trình: Đặt giá trị đầu tiên của chuỗi là n và biểu diễn các số tiếp theo dựa trên n. Sau đó, lập phương trình dựa vào điều kiện bài toán và giải phương trình để tìm n.
3. Tính chất đặc biệt: Lưu ý một số tính chất đặc biệt của chuỗi số nguyên liên tiếp, như tổng của m số nguyên liên tiếp chia hết cho m nếu m là số lẻ, hoặc tích của ba số nguyên liên tiếp chia hết cho 6.

Ví dụ minh họa:

• Tìm ba số nguyên liên tiếp có tổng là 51: Đặt số đầu tiên là x, ta có x + (x + 1) + (x + 2) = 51. Giải phương trình, ta tìm được x = 16, do đó ba số là 16, 17, và 18.
• Tìm hai số nguyên liên tiếp có tổng là 75: Biểu diễn hai số liên tiếp dưới dạng n và n+1, với tổng là 75. Giải phương trình tìm được n = 37, vậy hai số là 37 và 38.

Trong đại số, số nguyên liên tiếp đóng một vai trò quan trọng trong việc giải quyết nhiều loại bài toán khác nhau. Dưới đây là một số cách áp dụng số nguyên liên tiếp vào bài toán đại số:

• Số nguyên liên tiếp giúp xác định mối quan hệ giữa các số trong một chuỗi và tìm ra các đặc điểm chung của chuỗi số đó.
• Chúng được sử dụng để giải quyết các bài toán liên quan đến tổng, tích của một dãy số nhất định, như việc xác định tổng của các số nguyên liên tiếp hoặc tích của chúng.
• Áp dụng vào các bài toán liên quan đến tổng các số nguyên lẻ liên tiếp hoặc tổng các số nguyên chẵn liên tiếp.
• Giúp giải các bài toán tìm kiếm số nguyên dựa trên một số điều kiện nhất định, như tìm số nguyên sao cho tổng hoặc tích của chúng thỏa mãn điều kiện cho trước.

Ví dụ cụ thể:

1. Giải bài toán tìm ba số nguyên liên tiếp có tổng là 51: Dùng công thức x + (x + 1) + (x + 2) = 51, giải phương trình ta tìm được x = 16, từ đó suy ra ba số là 16, 17, và 18.
2. Giải bài toán tìm hai số nguyên liên tiếp có tổng là 75: Áp dụng công thức n + (n + 1) = 75, giải phương trình ta tìm được n = 37, suy ra hai số cần tìm là 37 và 38.

Qua những ví dụ trên, ta thấy rằng việc áp dụng số nguyên liên tiếp vào đại số không chỉ giúp giải quyết các bài toán một cách hiệu quả mà còn giúp chúng ta hiểu sâu sắc hơn về mối quan hệ giữa các số nguyên và ứng dụng của chúng trong toán học.

Trong đại số, số nguyên liên tiếp đóng một vai trò quan trọng trong việc giải quyết nhiều loại bài toán khác nhau. Dưới đây là một số cách áp dụng số nguyên liên tiếp vào bài toán đại số:

• Số nguyên liên tiếp giúp xác định mối quan hệ giữa các số trong một chuỗi và tìm ra các đặc điểm chung của chuỗi số đó.
• Chúng được sử dụng để giải quyết các bài toán liên quan đến tổng, tích của một dãy số nhất định, như việc xác định tổng của các số nguyên liên tiếp hoặc tích của chúng.
• Áp dụng vào các bài toán liên quan đến tổng các số nguyên lẻ liên tiếp hoặc tổng các số nguyên chẵn liên tiếp.
• Giúp giải các bài toán tìm kiếm số nguyên dựa trên một số điều kiện nhất định, như tìm số nguyên sao cho tổng hoặc tích của chúng thỏa mãn điều kiện cho trước.

Ví dụ cụ thể:

1. Giải bài toán tìm ba số nguyên liên tiếp có tổng là 51: Dùng công thức x + (x + 1) + (x + 2) = 51, giải phương trình ta tìm được x = 16, từ đó suy ra ba số là 16, 17, và 18.
2. Giải bài toán tìm hai số nguyên liên tiếp có tổng là 75: Áp dụng công thức n + (n + 1) = 75, giải phương trình ta tìm được n = 37, suy ra hai số cần tìm là 37 và 38.

Qua những ví dụ trên, ta thấy rằng việc áp dụng số nguyên liên tiếp vào đại số không chỉ giúp giải quyết các bài toán một cách hiệu quả mà còn giúp chúng ta hiểu sâu sắc hơn về mối quan hệ giữa các số nguyên và ứng dụng của chúng trong toán học.

Qua việc khám phá số nguyên liên tiếp, ta không chỉ cải thiện kỹ năng giải toán mà còn mở rộng tầm nhìn về vẻ đẹp của toán học, giúp ta liên kết lý thuyết với thực tiễn cuộc sống. Sự hiểu biết sâu sắc về chúng là bước đệm vững chắc cho những khám phá toán học tiếp theo.