Chủ đề consecutive numbers: Khám phá thế giới kỳ diệu của các số liên tiếp, nơi mỗi con số kể một câu chuyện và mở ra cánh cửa của bí ẩn toán học. Từ những quy luật đơn giản đến những ứng dụng phức tạp, bài viết này sẽ dẫn dắt bạn qua hành trình khám phá không chỉ là con số, mà còn là cảm hứng và sự tò mò. Hãy cùng chúng tôi bước vào thế giới của các số liên tiếp, nơi mọi khám phá đều bắt đầu từ những điều cơ bản nhất.
Mục lục
- Định Nghĩa
- Các Ví Dụ
- Thuộc Tính
- Công Thức
- Các tài liệu nào có thể giúp tôi hiểu rõ hơn về các số liên tiếp?
- YOUTUBE: Giải bài toán số nguyên liên tiếp bằng phương pháp đại số | Phương trình tuyến tính | Đại số I | Khan Academy
- Định Nghĩa Số Liên Tiếp
- Ví Dụ về Số Liên Tiếp
- Tính Chất của Số Liên Tiếp
- Công Thức và Cách Tính Số Liên Tiếp
- Ứng Dụng của Số Liên Tiếp Trong Toán Học và Cuộc Sống
- Các Bài Toán về Số Liên Tiếp
- Cách Giải và Lời Giải cho Các Bài Toán Số Liên Tiếp Phổ Biến
- Mẹo và Thủ Thuật Giải Bài Toán Số Liên Tiếp
Định Nghĩa
Số liên tiếp là những số nằm cạnh nhau trong một dãy số, chẳng hạn như 1, 2, 3 hoặc 10, 11, 12.
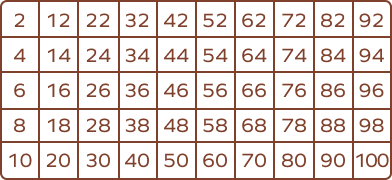
Các Ví Dụ
- 1, 2, 3 là một chuỗi các số nguyên liên tiếp.
- 22, 23, 24 cũng là một chuỗi các số nguyên liên tiếp.
Thuộc Tính
- Khoảng cách giữa mỗi cặp số liên tiếp luôn là 1.
- Nếu bạn lấy hai số nguyên liên tiếp, tổng của chúng luôn là một số lẻ.

Công Thức
Đối với hai số liên tiếp n và n+1, chúng ta có thể sử dụng công thức này để xác định các số tiếp theo.
Ví dụ về Số Chẵn Liên Tiếp
Nếu x là một số chẵn, thì x và x+2 là hai số chẵn liên tiếp.
Ví dụ về Số Lẻ Liên Tiếp
Ví dụ, 1, 3, 5, 7 và 9 là các số lẻ liên tiếp.
Các tài liệu nào có thể giúp tôi hiểu rõ hơn về các số liên tiếp?
Các tài liệu sau đây có thể giúp bạn hiểu rõ hơn về các số liên tiếp:
-
Trang web số học cơ bản: Truy cập vào các trang web giáo dục về số học cơ bản để tìm hiểu về khái niệm của các số liên tiếp.
-
Sách giáo trình toán học: Đọc các sách giáo trình toán học cấp độ phù hợp để hiểu cách xác định và tính toán các số liên tiếp.
-
Khóa học trực tuyến: Theo các khóa học trực tuyến về toán học hoặc lĩnh vực liên quan để được hướng dẫn chi tiết về các số liên tiếp.
-
Forum hoặc cộng đồng trực tuyến: Tham gia các diễn đàn hoặc cộng đồng trực tuyến về toán học để trao đổi kiến thức và giải đáp thắc mắc về các số liên tiếp.
Giải bài toán số nguyên liên tiếp bằng phương pháp đại số | Phương trình tuyến tính | Đại số I | Khan Academy
Hệ thống số và phương pháp đại số đều quan trọng trong cuộc sống. Số liên tiếp tạo nên sự liên tục, phát triển vững chắc. Khám phá thêm trên YouTube ngay!
Hệ thống số || Số liên tiếp (BÀI HỌC-7)
FeelFreetoLearn.
Định Nghĩa Số Liên Tiếp
Số liên tiếp là những số theo sau nhau trong một dãy số mà không có bất kỳ khoảng trống nào giữa chúng. Điều này có nghĩa là, mỗi số trong dãy liên tiếp lớn hơn số trước đó một đơn vị. Ví dụ, 1, 2, 3 hoặc 10, 11, 12 đều là các ví dụ về số liên tiếp.
- Số liên tiếp có thể bao gồm cả số chẵn và số lẻ.
- Chúng thường được sử dụng trong nhiều bài toán toán học khác nhau.
- Số liên tiếp bắt đầu từ một số nào đó và tiếp tục tăng dần một đơn vị.
- Khái niệm về số liên tiếp không chỉ giới hạn ở số nguyên mà còn có thể áp dụng cho các loại số khác.
| Số liên tiếp chẵn | 2, 4, 6, 8 |
| Số liên tiếp lẻ | 1, 3, 5, 7 |
| Số liên tiếp nguyên | -3, -2, -1, 0, 1 |

Ví Dụ về Số Liên Tiếp
Số liên tiếp là một khái niệm quan trọng trong toán học, dễ dàng tìm thấy trong cuộc sống hàng ngày. Dưới đây là một số ví dụ điển hình để giúp hiểu rõ hơn về số liên tiếp.
- 1, 2, 3, 4, 5: Một dãy số nguyên dương liên tiếp từ 1 đến 5.
- 0, 1, 2, 3, 4: Một dãy số nguyên liên tiếp bắt đầu từ 0.
- -2, -1, 0, 1, 2: Một dãy số liên tiếp bao gồm cả số nguyên âm và dương.
Các ví dụ trên thể hiện rằng số liên tiếp có thể bắt đầu từ bất kỳ điểm nào và tiếp tục theo một trật tự tăng dần hoặc giảm dần mà không bị gián đoạn.
- Trong toán học, việc nhận biết và sử dụng số liên tiếp giúp giải quyết nhiều bài toán.
- Số liên tiếp cũng được ứng dụng trong các lĩnh vực như khoa học máy tính, kỹ thuật và thống kê.
Tính Chất của Số Liên Tiếp
Số liên tiếp có một số tính chất đặc biệt giúp chúng ta nhận biết và áp dụng chúng trong nhiều bài toán khác nhau. Dưới đây là một số tính chất nổi bật.
- Mỗi số trong dãy liên tiếp lớn hơn số trước đó một đơn vị.
- Tổng của hai số liên tiếp luôn là một số lẻ.
- Hiệu của hai số liên tiếp luôn bằng 1.
Các tính chất này giúp chúng ta dễ dàng xác định và sử dụng số liên tiếp trong nhiều tình huống toán học và ứng dụng thực tế.
- Tính chất chia hết: Khi chia số liên tiếp cho một số nào đó, kết quả sẽ tuân theo một quy luật nhất định.
- Tính chất đối xứng: Trong một dãy số liên tiếp nhất định, có thể tìm thấy tính chất đối xứng qua một số hoặc một nhóm số.
| Tính chất | Ví dụ |
| Tổng của hai số liên tiếp | 1 + 2 = 3 (số lẻ) |
| Hiệu của hai số liên tiếp | 3 - 2 = 1 |
Công Thức và Cách Tính Số Liên Tiếp
Để tính và xác định số liên tiếp trong một dãy số, có thể sử dụng một số công thức cơ bản. Công thức giúp ta dễ dàng tìm ra số tiếp theo hoặc toàn bộ dãy số liên tiếp từ một số cho trước.
- Để tìm số liên tiếp sau một số n: Sử dụng công thức n + 1.
- Để tạo dãy số liên tiếp bắt đầu từ một số bất kỳ: Bắt đầu từ số đó và áp dụng công thức n + 1 cho mỗi bước tiếp theo.
Áp dụng các công thức này giúp ta nhanh chóng xác định và tạo dãy số liên tiếp trong nhiều tình huống khác nhau.
- Đối với dãy số liên tiếp chẵn hoặc lẻ, có thể sử dụng công thức n + 2 bắt đầu từ số chẵn hoặc lẻ đầu tiên.
- Để tính tổng của một dãy số liên tiếp, sử dụng công thức tổng = n(n + 1) / 2, với n là số lượng số liên tiếp.
Ứng Dụng của Số Liên Tiếp Trong Toán Học và Cuộc Sống
Số liên tiếp không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các lĩnh vực khoa học khác. Dưới đây là một số ứng dụng nổi bật.
- Trong toán học: Số liên tiếp được sử dụng để giải các bài toán liên quan đến dãy số, tổng số, và nhiều khái niệm khác.
- Trong khoa học máy tính: Dãy số liên tiếp giúp trong việc phát triển các thuật toán và xử lý dữ liệu hiệu quả.
- Trong cuộc sống hàng ngày: Số liên tiếp được dùng để đánh số trang trong sách, đánh số nhà, và nhiều hoạt động khác.
Các ứng dụng này chỉ ra rằng, số liên tiếp có vai trò quan trọng không chỉ trong lĩnh vực toán học mà còn trong nhiều khía cạnh khác của đời sống.
- Ứng dụng trong giáo dục: Giúp trẻ em nhận biết về số lượng và thứ tự.
- Ứng dụng trong kỹ thuật: Xác định thứ tự thực hiện các bước trong một quy trình.
| Lĩnh vực | Ví dụ Ứng Dụng |
| Toán học | Tìm tổng của dãy số liên tiếp |
| Khoa học máy tính | Sắp xếp dữ liệu |
| Cuộc sống hàng ngày | Đánh số trang sách |

Các Bài Toán về Số Liên Tiếp
Số liên tiếp là một chủ đề quan trọng trong toán học, với ứng dụng rộng rãi trong giải quyết các bài toán từ cơ bản đến nâng cao. Dưới đây là một số ví dụ về bài toán liên quan đến số liên tiếp.
- Tìm tổng của một dãy số liên tiếp.
- Giải bài toán về số liên tiếp trong các dãy số toán học như dãy Fibonacci.
- Xác định số lượng số liên tiếp cần thiết để đạt được một tổng cụ thể.
Các bài toán này giúp rèn luyện tư duy toán học và kỹ năng giải quyết vấn đề trong nhiều tình huống.
- Đề bài: Cho một dãy số liên tiếp bắt đầu từ 1, tìm tổng của 10 số đầu tiên.
- Giải pháp: Sử dụng công thức tổng của dãy số liên tiếp là n(n + 1)/2.
Cách Giải và Lời Giải cho Các Bài Toán Số Liên Tiếp Phổ Biến
Các bài toán về số liên tiếp có thể giải theo nhiều cách khác nhau tùy thuộc vào đặc điểm của bài toán. Dưới đây là một số phương pháp giải quyết chung và lời giải cho các bài toán số liên tiếp phổ biến.
- Phương pháp sử dụng công thức toán học: Áp dụng công thức n(n + 1)/2 để tính tổng của dãy số liên tiếp.
- Phương pháp phân tích: Chia nhỏ bài toán và giải quyết từng phần.
- Phương pháp thử và sai: Thử các giả thuyết khác nhau và kiểm tra kết quả.
Áp dụng các phương pháp trên giúp giải quyết hiệu quả các bài toán số liên tiếp từ cơ bản đến phức tạp.
- Bài toán: Tìm tổng của dãy số liên tiếp từ 1 đến n.
- Lời giải: Sử dụng công thức tổng của dãy số liên tiếp là n(n + 1)/2.
| Bài toán | Phương pháp giải | Lời giải |
| Tổng của dãy số liên tiếp từ 1 đến 100 | Áp dụng công thức | 5050 |
| Xác định số số liên tiếp cần thiết để đạt tổng 100 | Phân tích và thử nghiệm | Áp dụng các kỹ thuật giải toán để xác định |

Mẹo và Thủ Thuật Giải Bài Toán Số Liên Tiếp
Giải bài toán số liên tiếp không chỉ dựa vào kiến thức toán học mà còn cần sự khéo léo và áp dụng một số mẹo, thủ thuật sau đây:
- Luôn bắt đầu bằng việc xác định rõ ràng dãy số liên tiếp bạn đang làm việc với nó. Điều này giúp hạn chế sai sót.
- Sử dụng công thức tổng của dãy số liên tiếp n(n + 1)/2 để nhanh chóng tìm tổng mà không cần tính từng số.
- Đối với bài toán tìm số lượng số liên tiếp cần thiết để đạt một tổng nhất định, hãy thử áp dụng phương pháp loại trừ dựa trên tính chất của số liên tiếp.
Áp dụng những mẹo này không chỉ giúp giải quyết bài toán một cách hiệu quả mà còn phát triển tư duy toán học.
- Khi giải các bài toán phức tạp, hãy chia nhỏ chúng thành nhiều phần nhỏ hơn có thể giải quyết riêng biệt.
- Luôn kiểm tra lại công thức và kết quả của mình để tránh những sai lầm không đáng có.
Khám phá thế giới của số liên tiếp mở ra cánh cửa vào những hiểu biết sâu sắc về toán học và ứng dụng thực tế trong cuộc sống. Từ giải quyết bài toán đến việc áp dụng trong các tình huống thực tế, số liên tiếp là khái niệm không thể thiếu, giúp chúng ta tiếp cận với vẻ đẹp của toán học một cách linh hoạt và sáng tạo.