Chủ đề transitive elements: Khám phá thế giới kỳ diệu của "transitive elements" trong toán học và các ứng dụng không ngờ tới trong cuộc sống hàng ngày. Từ logic đến hình học, chúng tôi sẽ dẫn dắt bạn qua những khám phá thú vị, giúp bạn hiểu rõ hơn về cách thức quan hệ transitive tạo nên nền móng cho nhiều lĩnh vực khoa học. Hãy cùng chúng tôi khai mở bí mật đằng sau các quan hệ này và ứng dụng chúng vào thực tiễn.
Mục lục
- Các quan hệ Transitive trong Toán học
- Bạn muốn tìm hiểu về những yếu tố transitive trong lĩnh vực nào khi tìm kiếm transitive elements trên Google?
- YOUTUBE: Transitive Elements - Làm Tôi Cảm Thấy Tốt (Chưa Phát Hành) 1994 UMM
- Định nghĩa và ý nghĩa của quan hệ Transitive
- Tính chất của quan hệ Transitive
- Ví dụ về quan hệ Transitive
- Ví dụ về quan hệ Transitive trong thực tế và toán học
- Tính chất và đặc điểm của các quan hệ Transitive
- Ứng dụng của quan hệ Transitive trong lĩnh vực khác nhau
- Cách xác định và kiểm tra quan hệ Transitive
- So sánh quan hệ Transitive với các quan hệ khác: Reflexive và Symmetric
- Câu hỏi thường gặp và giải đáp về quan hệ Transitive
Các quan hệ Transitive trong Toán học
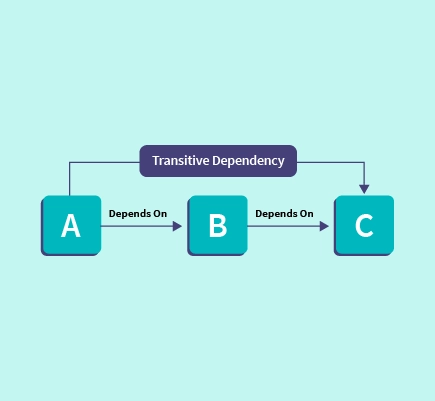
Một quan hệ R trên một tập hợp A được gọi là transitive nếu mọi a, b, c trong A, từ a R b và b R c suy ra a R c.
Định nghĩa
Quan hệ transitive có thể được áp dụng cho số, biểu thức đại số, và nhiều khái niệm hình học khác.
Ví dụ
- "Bằng nhau" là một quan hệ transitive trên tập số thực. Nếu a = b và b = c, thì a = c.
- "Lớn hơn" và "Lớn hơn hoặc bằng" là các quan hệ transitive trên tập số thực.
Tính chất
- Đảo ngược của một quan hệ transitive cũng là một quan hệ transitive.
- Giao điểm của hai quan hệ transitive cũng là một quan hệ transitive.
- Liên kết của hai quan hệ transitive không nhất thiết phải là transitive.
Một số vấn đề liên quan
Quan hệ được định nghĩa trên một tập hợp rỗng luôn luôn là transitive.
Không có công thức cố định để xác định số lượng quan hệ transitive trên một tập hợp.
| Quan hệ | Transitive? |
| Bằng nhau (=) | Có |
| Khác nhau (!=) | Không |
Câu hỏi thường gặp
Quan hệ transitive trong lý thuyết tập hợp là gì? Là một quan hệ nhị phân trên tập B sao cho nếu a liên quan đến b và b liên quan đến c, với mọi a, b, c trong B, thì a cũng phải liên quan đến c.
Bạn muốn tìm hiểu về những yếu tố transitive trong lĩnh vực nào khi tìm kiếm transitive elements trên Google?
Trong quá trình tìm kiếm trên Google với keyword "transitive elements", có thể bạn đang quan tâm đến yếu tố transitive trong lĩnh vực ngôn ngữ học hoặc toán học.
Dưới đây là một số lĩnh vực mà transitive elements có thể được áp dụng:
- Ngôn ngữ học: Trong ngữ pháp học, transitive elements thường được sử dụng để nói về mối quan hệ giữa các thành phần trong câu, như động từ, chủ ngữ và tân ngữ.
- Toán học: Trong đại số, transitive elements thường được xem xét trong ngữ cảnh của các phép toán và quan hệ transitive giữa các phần tử của một tập hợp.
Việc tìm hiểu về transitive elements trong các lĩnh vực này có thể giúp bạn hiểu rõ hơn về tính chất và ứng dụng của chúng trong ngôn ngữ học và toán học.
Transitive Elements - Làm Tôi Cảm Thấy Tốt (Chưa Phát Hành) 1994 UMM
Âm nhạc không chỉ là khám phá âm thanh mà còn là sự kết hợp tinh tế giữa hòa âm và lời ca, tạo nên một mối quan hệ bắc quy đầy bất ngờ và cuốn hút.
Mối Quan Hệ Bắc Quy (Transitive Relations) | Cách Xác Định Một Mối Quan Hệ Có Bắc Quy Hay Không (Ví dụ 1)
Following this channel's introductory video to transitive relations, this video goes through an example of how to determine if a ...
Định nghĩa và ý nghĩa của quan hệ Transitive
Trong toán học, quan hệ Transitive là một khái niệm quan trọng trong lý thuyết tập hợp và logic. Một quan hệ được gọi là Transitive nếu và chỉ nếu cho mọi a, b, c thuộc vào một tập hợp, từ "a có quan hệ với b" và "b có quan hệ với c" ta có thể suy ra "a có quan hệ với c".
Ví dụ, quan hệ "lớn hơn" là transitive: nếu a > b và b > c, thì chắc chắn a > c. Điều này áp dụng cho các quan hệ khác như "bằng", "lớn hơn hoặc bằng", và nhiều quan hệ khác trong toán học.
Tính chất của quan hệ Transitive
- Mọi quan hệ đều có khả năng là transitive, nhưng không phải luôn luôn vậy.
- Quan hệ đảo ngược của một quan hệ transitive cũng là transitive.
- Giao điểm của hai quan hệ transitive cũng là một quan hệ transitive.

Ví dụ về quan hệ Transitive
- Nếu "a bằng b" và "b bằng c", thì "a bằng c".
- Nếu "a lớn hơn b" và "b lớn hơn c", thì "a lớn hơn c".
Quan hệ transitive đóng một vai trò quan trọng trong việc xây dựng và hiểu các định lý toán học, đặc biệt là trong lý thuyết tập hợp và logic.
Qua bảng trên, chúng ta có thể thấy sự khác biệt giữa các quan hệ và nhận biết được đâu là quan hệ transitive.
Ví dụ về quan hệ Transitive trong thực tế và toán học
Quan hệ Transitive xuất hiện rộng rãi trong cả thực tế và toán học, giúp chúng ta hiểu rõ hơn về cấu trúc và mối liên hệ giữa các phần tử.
- Trong cuộc sống hàng ngày, quan hệ "là anh chị em ruột" thể hiện tính chất transitive: Nếu người A là anh chị em ruột của người B, và B là anh chị em ruột của C, thì A cũng là anh chị em ruột của C.
- Trong toán học, "nhỏ hơn" (<) và "bằng" (=) là các ví dụ điển hình về quan hệ transitive. Ví dụ, nếu a < b và b < c, thì a < c; nếu a = b và b = c, thì a = c.
- Quan hệ "đồng dạng" giữa các hình học cũng là một quan hệ transitive: Nếu hình tam giác ABC đồng dạng với tam giác PQR, và PQR đồng dạng với XYZ, thì ABC đồng dạng với XYZ.
Những ví dụ trên giúp chúng ta thấy được tính ứng dụng rộng rãi và quan trọng của quan hệ transitive trong việc phân tích và giải quyết các vấn đề trong cả toán học và đời sống.

Tính chất và đặc điểm của các quan hệ Transitive
Quan hệ Transitive là một khái niệm cơ bản trong lý thuyết tập hợp và toán học, áp dụng cho các mối quan hệ nhị phân trên một tập hợp. Đặc điểm chính của quan hệ này là sự chuyển tiếp: nếu một phần tử a liên quan đến b và b liên quan đến c, thì a cũng phải liên quan đến c.
- Đảo ngược của một quan hệ transitive cũng là một quan hệ transitive. Ví dụ, nếu "nhỏ hơn" là một quan hệ transitive, thì "lớn hơn" cũng là một quan hệ transitive.
- Giao điểm của hai quan hệ transitive cũng là một quan hệ transitive. Tuy nhiên, sự hợp nhất của hai quan hệ transitive không nhất thiết phải là transitive.
- Một quan hệ transitive là một quan hệ không đối xứng chỉ khi nó là không phản xạ.
- Quan hệ transitive có thể phản xạ, tức là mọi phần tử chỉ liên quan đến chính nó.
Một số ví dụ phổ biến về quan hệ transitive bao gồm "là một tập con của", "nhỏ hơn", "bằng", và "đồng dạng với". Quan hệ không transitive bao gồm "là cha mẹ ruột của" và "đứng cạnh".
| Quan hệ | Transitive | Anti-Transitive |
| Nhỏ hơn | Có | Không |
| Bằng | Có | Không |
| Là cha mẹ ruột của | Không | Có |
Những tính chất này giúp định hình và hiểu biết về cách quan hệ transitive hoạt động trong toán học và logic.
Ứng dụng của quan hệ Transitive trong lĩnh vực khác nhau
Quan hệ Transitive là một nền tảng cơ bản trong toán học, nhưng ứng dụng của nó vượt ra ngoài và được tìm thấy trong nhiều lĩnh vực khác nhau.
- Toán học và Lập trình: Dùng để chứng minh tính chất và xây dựng thuật toán, đặc biệt trong lý thuyết đồ thị và cơ sở dữ liệu.
- Khoa học máy tính: Trong quản lý cơ sở dữ liệu, quan hệ transitive giúp thiết lập mối liên kết giữa các đối tượng và tối ưu hóa truy vấn.
- Triết học và Logic: Dùng để xây dựng và chứng minh các lập luận logic, là nền tảng của lý luận và suy diễn.
- Xã hội học và Tâm lý học: Nghiên cứu mối quan hệ giữa các cá nhân và nhóm, chẳng hạn như quan hệ gia đình hoặc mối quan hệ xã hội.
- Quản lý và Tổ chức: Trong quản lý dự án và cấu trúc tổ chức, giúp xác định mối quan hệ giữa các công việc và quy trình.
Qua đó, có thể thấy quan hệ Transitive không chỉ giới hạn trong toán học mà còn ảnh hưởng và được ứng dụng trong nhiều ngành nghề và lĩnh vực khác của đời sống.
Cách xác định và kiểm tra quan hệ Transitive
Quan hệ transitive là một khái niệm cốt lõi trong lý thuyết quan hệ, và việc xác định liệu một quan hệ có là transitive hay không là quan trọng trong nhiều lĩnh vực của toán học và khoa học máy tính.
- Định nghĩa: Một quan hệ R trên tập hợp A được gọi là transitive nếu, với mọi a, b, c thuộc A, từ aRb và bRc suy ra aRc.
- Quy trình kiểm tra:
- Liệt kê tất cả các cặp phần tử (a, b) và (b, c) trong quan hệ R.
- Kiểm tra xem với mọi cặp (a, b) và (b, c) tìm thấy, cặp (a, c) có nằm trong quan hệ R không.
- Nếu tất cả các cặp (a, c) tương ứng đều thuộc R, thì quan hệ đó là transitive.
- Nếu có bất kỳ cặp (a, c) nào không thuộc R trong khi (a, b) và (b, c) thuộc R, thì quan hệ đó không phải là transitive.
Lưu ý: Một số quan hệ có thể không rõ ràng là transitive từ ban đầu, nên cần phải xem xét kỹ lưỡng tất cả các phần tử trong quan hệ đó.
Hãy áp dụng quy trình này để kiểm tra tính transitive cho mọi quan hệ bạn gặp phải trong toán học hoặc trong các bài toán thực tế.
So sánh quan hệ Transitive với các quan hệ khác: Reflexive và Symmetric
Trong toán học, quan hệ Transitive, Reflexive và Symmetric là những khái niệm cơ bản của lý thuyết quan hệ. Mỗi quan hệ có đặc điểm và ứng dụng riêng biệt.
- Quan hệ Reflexive: Một quan hệ được gọi là Reflexive nếu mọi phần tử trong tập A có mối quan hệ với chính nó, tức là, ∀a ∈ A, aRa. Ví dụ, quan hệ "bằng" trong tập số thực là một quan hệ reflexive vì mọi số đều bằng chính nó.
- Quan hệ Symmetric: Một quan hệ được coi là Symmetric nếu bất kỳ khi nào a có quan hệ với b, thì b cũng có quan hệ với a, tức là, ∀a, b ∈ A, nếu aRb thì bRa. Ví dụ, quan hệ "có cùng tuổi" giữa các cá nhân là symmetric.
- Quan hệ Transitive: Một quan hệ được xem là Transitive nếu bất kỳ khi nào a có quan hệ với b và b có quan hệ với c, thì a cũng có quan hệ với c, tức là, ∀a, b, c ∈ A, nếu aRb và bRc thì aRc. Ví dụ, "lớn hơn" là một quan hệ transitive.
So sánh:
| Quan hệ | Reflexive | Symmetric | Transitive |
| Bằng | Có | Có | Có |
| Lớn hơn | Không | Không | Có |
| Có cùng tuổi | Có | Có | Không nhất thiết |
Qua so sánh, chúng ta có thể thấy mỗi quan hệ có những tính chất đặc thù riêng biệt. Quan hệ Transitive thường liên quan đến sự sắp xếp hoặc thứ tự, trong khi Reflexive và Symmetric liên quan nhiều hơn đến sự tương đồng và đối xứng.

Câu hỏi thường gặp và giải đáp về quan hệ Transitive
- Câu hỏi: Quan hệ transitive là gì?
- Trả lời: Quan hệ transitive trong toán học là một quan hệ giữa ba phần tử sao cho nếu một phần tử liên quan đến phần tử thứ hai và phần tử thứ hai liên quan đến phần tử thứ ba, thì phần tử đầu tiên cũng liên quan đến phần tử thứ ba.
- Câu hỏi: Làm thế nào để kiểm tra một quan hệ có phải là transitive không?
- Trả lời: Để kiểm tra một quan hệ có phải là transitive, ta xem xét tất cả các cặp phần tử (a, b) và (b, c) trong quan hệ đó. Nếu mỗi khi cặp này tồn tại, cặp (a, c) cũng tồn tại trong quan hệ, thì quan hệ đó là transitive.
- Câu hỏi: Một quan hệ có thể vừa là transitive vừa không transitive được không?
- Trả lời: Một quan hệ không thể vừa là transitive vừa không transitive. Nó hoặc tuân theo tính chất transitive hoặc không.
- Câu hỏi: Có ví dụ nào về quan hệ transitive trong đời sống thực không?
- Trả lời: Ví dụ, quan hệ "lớn hơn" giữa các số là một quan hệ transitive: nếu a > b và b > c, thì chắc chắn là a > c.
- Câu hỏi: Một quan hệ có thể là transitive nhưng không phản xạ hoặc đối xứng được không?
- Trả lời: Có, ví dụ, quan hệ "lớn hơn" là transitive nhưng không phản xạ (không phần tử nào lớn hơn chính nó) và không đối xứng (nếu a > b thì không có nghĩa là b > a).
Khám phá thế giới kỳ diệu của các quan hệ Transitive mở ra cánh cửa mới để hiểu biết và ứng dụng trong toán học và cuộc sống. Đừng ngần ngại khai thác và áp dụng kiến thức này vào giải quyết các vấn đề phức tạp, nâng cao hiểu biết và khả năng tư duy logic của bạn.