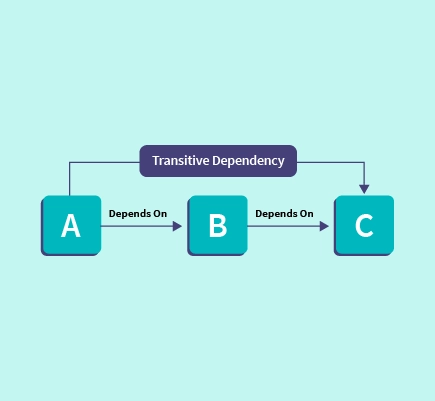
Chủ đề transitive property: Khám phá "Tính chất chuyển tiếp" - một khái niệm toán học không chỉ quan trọng trong lý thuyết mà còn ứng dụng trong cuộc sống hàng ngày. Từ giải quyết phương trình đến hiểu biết về mối quan hệ giữa các hình học, tính chất này mở ra cánh cửa của hiểu biết và sáng tạo. Hãy cùng chúng tôi khám phá sức mạnh và vẻ đẹp ẩn sau nó!
Mục lục
- Tính chất chuyển tiếp
- Giới thiệu về Tính chất chuyển tiếp
- Tính chất nào của transitive property thường được áp dụng trong các hệ phương trình?
- YOUTUBE: Tính chất \item Chuyển hoán và \item Thay thế trong hình \item Đẳng thức
- Định nghĩa Tính chất chuyển tiếp
- Các ví dụ về Tính chất chuyển tiếp
- Tính chất chuyển tiếp trong Đại số
- Tính chất chuyển tiếp của Bất đẳng thức
- Tính chất chuyển tiếp trong Hình học
- Ứng dụng của Tính chất chuyển tiếp
- Câu hỏi thường gặp và giải đáp
- Tài liệu tham khảo và bài tập thực hành
Tính chất chuyển tiếp
Tính chất chuyển tiếp là một khái niệm cơ bản trong toán học, được áp dụng cho cả đẳng thức và bất đẳng thức.
Tính chất chuyển tiếp của đẳng thức
Theo tính chất chuyển tiếp của đẳng thức, nếu \(a = b\) và \(b = c\), thì \(a = c\).
- Ví dụ: Nếu \(a = b\), \(b = c\), và \(c = 2\), thì \(a = b = c = 2\).
Tính chất chuyển tiếp của bất đẳng thức
Theo tính chất chuyển tiếp của bất đẳng thức:
- Nếu \(a < b\) và \(b < c\), thì \(a < c\).
- Nếu \(a > b\) và \(b > c\), thì \(a > c\).
- Nếu \(a \leq b\) và \(b \leq c\), thì \(a \leq c\).
- Nếu \(a \geq b\) và \(b \geq c\), thì \(a \geq c\).
Tính chất chuyển tiếp của đồng dạng
Tính chất chuyển tiếp cũng được áp dụng cho các hình học, ví dụ: nếu hai hình có cùng kích thước và hình dạng với một hình thứ ba, thì chúng cũng có cùng kích thước và hình dạng với nhau.
- Nếu ΔABC ≅ ΔPQR và ΔPQR ≅ ΔXYZ, thì ΔABC ≅ ΔXYZ.
Câu hỏi thường gặp về Tính chất chuyển tiếp
- Tính chất chuyển tiếp được sử dụng khi nào? Khi chúng ta có ba hoặc nhiều hơn ba lượng thuộc cùng một loại và được liên kết bằng một quy tắc.
- Khác biệt giữa Tính chất chuyển tiếp và Tính chất thay thế là gì? Tính chất thay thế cho phép một biểu thức thay thế cho một biểu thức khác có cùng giá trị, trong khi Tính chất chuyển tiếp liên quan đến việc so sánh ba lượng với nhau.

Giới thiệu về Tính chất chuyển tiếp
Tính chất chuyển tiếp, còn được biết đến với cái tên là tính chất chuyển tiếp của đẳng thức, là một nguyên tắc cơ bản trong toán học, phát biểu rằng nếu hai giá trị bằng nhau, và một trong hai giá trị đó bằng với một giá trị thứ ba, thì tất cả các giá trị đều bằng nhau.
Ví dụ, xem xét các biến a, b, và c đại diện cho cùng một số. Tính chất chuyển tiếp được biểu diễn như sau:
- Nếu \(a = b\) và \(b = c\), thì \(a = c\).
Tính chất này không chỉ áp dụng với số học mà còn trong nhiều lĩnh vực khác như đại số, hình học và logic.
Ứng dụng cụ thể:
- Trong Đại số: Nếu \(x = y\) và \(y = 2\), chúng ta có thể kết luận \(x = 2\).
- Trong Hình học: Nếu hai hình A và B đồng dạng với hình C, thì A và B cũng đồng dạng với nhau.
Bên cạnh đó, tính chất chuyển tiếp cũng được mở rộng ra với bất đẳng thức, giúp giải quyết các vấn đề phức tạp trong toán học và ứng dụng thực tế.
| Ký hiệu | Giải thích |
| \(a = b\) | 'a' bằng 'b' |
| \(b = c\) | 'b' bằng 'c' |
| \(a = c\) | Do đó, 'a' bằng 'c' |
Tính chất nào của transitive property thường được áp dụng trong các hệ phương trình?
Trong các hệ phương trình, tính chất quan trọng của transitive property thường được áp dụng là tính chất kế thừa. Để hiểu rõ hơn:
- Trước tiên, chúng ta cần biết rằng transitive property là một trong ba tính chất cơ bản của quan hệ tương đương trong toán học.
- Tính chất này nói rằng nếu a tương đương với b và b tương đương với c, thì ta có thể kết luận được rằng a cũng tương đương với c.
- Trong hệ phương trình, khi áp dụng transitive property, chúng ta thường sử dụng nó để chứng minh các bước trung gian trong quá trình giải phương trình, từ đó dẫn đến việc tìm ra nghiệm cuối cùng.
- Ví dụ, nếu từ phương trình 1 ta suy ra phương trình 2, và từ phương trình 2 suy ra phương trình 3, thì áp dụng transitive property sẽ giúp chúng ta kết luận được rằng phương trình 1 cũng tương đương với phương trình 3.
Tính chất \item Chuyển hoán và \item Thay thế trong hình \item Đẳng thức
Hãy khám phá video hấp dẫn về Điều Kiện Chuyển Hoán và Điều Kiện Thay Thế trong Hình Đẳng Thức Chuyển Tiếp. Hiểu biết sâu sắc và học hỏi mỗi ngày.
Tính chất \item Chuyển hoán trong hình \item Đẳng thức - Trợ giúp Toán học - Trợ giúp Toán học
For a complete lesson on the properties of equality, go to https://www.MathHelp.com - 1000+ online math lessons featuring a ...
Định nghĩa Tính chất chuyển tiếp
Tính chất chuyển tiếp, còn gọi là tính chất chuyển tiếp của đẳng thức, là một trong những nền tảng cơ bản của toán học. Nó mô tả mối quan hệ giữa ba yếu tố hoặc hơn, khẳng định rằng nếu một yếu tố bằng với yếu tố thứ hai và yếu tố thứ hai này lại bằng với yếu tố thứ ba, thì yếu tố đầu tiên và thứ ba cũng bằng nhau.
Trong ngôn ngữ toán học, điều này được biểu thị như sau:
- Nếu \(a = b\) và \(b = c\), thì \(a = c\).
Đây không chỉ là một khái niệm trừu tượng mà còn được áp dụng trong nhiều tình huống thực tế, từ giải phương trình đến chứng minh định lý trong hình học.
Những kiểu biểu diễn của Tính chất chuyển tiếp:
Tính chất này đóng một vai trò quan trọng trong việc xây dựng và chứng minh nhiều định lý toán học, giúp chúng ta kết nối và mở rộng các khái niệm từ đơn giản đến phức tạp.

Các ví dụ về Tính chất chuyển tiếp
Dưới đây là một số ví dụ cụ thể minh họa cho Tính chất chuyển tiếp trong các tình huống khác nhau:
- Ví dụ về Đẳng thức: Nếu chúng ta có \(a = b\) và \(b = c\), theo Tính chất chuyển tiếp, chúng ta có thể kết luận \(a = c\). Ví dụ, nếu \(x = 5\) và \(5 = y\), thì chúng ta có thể khẳng định \(x = y\).
- Ví dụ về Bất đẳng thức: Nếu \(a > b\) và \(b > c\), theo Tính chất chuyển tiếp, \(a > c\). Điều này giúp chúng ta so sánh trực tiếp giữa \(a\) và \(c\) mà không cần xem xét giá trị cụ thể của \(b\).
- Ví dụ trong Hình học: Giả sử rằng hai tam giác ΔABC và ΔDEF có cùng kích thước và hình dạng. Nếu ΔDEF đồng dạng với một tam giác khác ΔXYZ, thì theo Tính chất chuyển tiếp, ΔABC cũng đồng dạng với ΔXYZ.
Bảng sau đây tóm tắt các ví dụ đã nêu:
| Loại | Ví dụ | Kết luận |
| Đẳng thức | \(x = 5\), \(5 = y\) | \(x = y\) |
| Bất đẳng thức | \(a > b\), \(b > c\) | \(a > c\) |
| Hình học | ΔABC ≅ ΔDEF, ΔDEF ≅ ΔXYZ | ΔABC ≅ ΔXYZ |
Các ví dụ trên giúp chúng ta hiểu rõ hơn về việc áp dụng Tính chất chuyển tiếp trong toán học và trong các tình huống thực tế.
Tính chất chuyển tiếp trong Đại số
Tính chất chuyển tiếp đóng một vai trò quan trọng trong Đại số, giúp chúng ta giải quyết các phương trình và biểu diễn các quan hệ giữa các biến số một cách chính xác hơn.
Dưới đây là một số bước sử dụng Tính chất chuyển tiếp trong Đại số:
- Đặt các biểu thức hoặc phương trình đã biết có quan hệ bằng nhau.
- Sử dụng tính chất chuyển tiếp để thiết lập một quan hệ mới giữa các biểu thức chưa được trực tiếp so sánh.
- Sử dụng kết quả để giải quyết bài toán hoặc chứng minh một định lý.
Ví dụ minh họa:
- Nếu bạn có \(3x + 3 = 5x - 1\), bạn có thể sắp xếp lại để có \(3x + 3 = 5x - 1\).
- Tiếp theo, giải phương trình để tìm \(x\), bạn sẽ có \(-2x = -4\) và từ đó suy ra \(x = 2\).
Trong ví dụ trên, chúng tôi đã sử dụng Tính chất chuyển tiếp để thiết lập một mối quan hệ giữa \(3x + 3\) và \(5x - 1\) và sau đó giải quyết để tìm giá trị của \(x\).
Thông qua việc áp dụng Tính chất chuyển tiếp, chúng ta có thể đơn giản hóa và giải quyết nhiều vấn đề phức tạp trong Đại số.

Tính chất chuyển tiếp của Bất đẳng thức
Tính chất chuyển tiếp của Bất đẳng thức giúp chúng ta hiểu và giải quyết các bài toán bất đẳng thức một cách logic và có hệ thống. Nó áp dụng cho cả bốn dạng bất đẳng thức: nhỏ hơn, lớn hơn, nhỏ hơn hoặc bằng, và lớn hơn hoặc bằng.
Định nghĩa:
- Nếu \(a < b\) và \(b < c\), thì \(a < c\).
- Nếu \(a > b\) và \(b > c\), thì \(a > c\).
- Nếu \(a \leq b\) và \(b \leq c\), thì \(a \leq c\).
- Nếu \(a \geq b\) và \(b \geq c\), thì \(a \geq c\).
Ví dụ minh họa:
- Giả sử bạn có \(2 < 5\) và \(5 < 10\), từ đó bạn có thể kết luận \(2 < 10\) dựa trên tính chất chuyển tiếp.
- Nếu một học sinh có chiều cao nhỏ hơn chiều cao trung bình của lớp (\(h < H\)) và chiều cao trung bình của lớp nhỏ hơn chiều cao của giáo viên (\(H < G\)), thì chiều cao của học sinh đó cũng nhỏ hơn chiều cao của giáo viên (\(h < G\)).
Bảng sau đây tóm tắt cách áp dụng Tính chất chuyển tiếp trong bất đẳng thức:
| Loại Bất đẳng thức | Ví dụ | Kết luận |
| Nhỏ hơn | \(2 < 5\), \(5 < 10\) | \(2 < 10\) |
| Lớn hơn | \(10 > 5\), \(5 > 2\) | \(10 > 2\) |
| Nhỏ hơn hoặc bằng | \(3 \leq 4\), \(4 \leq 5\) | \(3 \leq 5\) |
| Lớn hơn hoặc bằng | \(5 \geq 4\), \(4 \geq 3\) | \(5 \geq 3\) |
Thông qua việc hiểu và áp dụng Tính chất chuyển tiếp của Bất đẳng thức, chúng ta có thể giải quyết nhiều vấn đề liên quan đến so sánh và xếp hạng trong toán học và các tình huống thực tế.
Tính chất chuyển tiếp trong Hình học
Tính chất chuyển tiếp trong Hình học giúp chúng ta hiểu và chứng minh mối quan hệ giữa các hình, góc, đoạn thẳng và các đối tượng hình học khác. Điều này đặc biệt quan trọng trong việc thiết lập sự đồng dạng và bằng nhau giữa các hình khác nhau.
Dưới đây là cách áp dụng Tính chất chuyển tiếp trong Hình học:
- Chứng minh hai hình (hoặc đoạn thẳng, góc, ...) bằng nhau hoặc đồng dạng với một hình thứ ba.
- Sử dụng tính chất chuyển tiếp để kết luận hai hình đó cũng bằng nhau hoặc đồng dạng với nhau.
Ví dụ cụ thể:
- Nếu ∠A = ∠B và ∠B = ∠C, theo Tính chất chuyển tiếp, ∠A = ∠C.
- Nếu đoạn thẳng AB đồng dạng với đoạn thẳng CD và CD đồng dạng với EF, thì AB cũng đồng dạng với EF.
Bảng sau đây minh họa một số ứng dụng của Tính chất chuyển tiếp trong Hình học:
Tính chất chuyển tiếp được sử dụng rộng rãi trong việc giải quyết các bài toán và chứng minh trong Hình học, từ đơn giản đến phức tạp, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố hình học.

Ứng dụng của Tính chất chuyển tiếp
Tính chất chuyển tiếp không chỉ quan trọng trong toán học mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác, từ khoa học tự nhiên đến khoa học xã hội. Dưới đây là một số ứng dụng cụ thể của Tính chất chuyển tiếp:
- Trong Đại số, giúp giải các phương trình và hệ phương trình, tạo điều kiện để tìm ra giá trị của các biến.
- Trong Hình học, chứng minh sự bằng nhau hoặc đồng dạng giữa các hình, giúp giải các bài toán về đo lường và cấu trúc.
- Trong Lập luận và Chứng minh toán học, xác lập các mối quan hệ giữa các đối tượng toán học và chứng minh tính đúng đắn của các định lý.
- Trong Khoa học máy tính, xây dựng và kiểm chứng các thuật toán, đặc biệt là trong lĩnh vực lý thuyết đồ thị và cơ sở dữ liệu.
- Trong Kinh tế học, phân tích và so sánh các mối quan hệ giữa các yếu tố kinh tế như giá cả, sản lượng và thu nhập.
Bảng sau đây tóm tắt một số ứng dụng cụ thể:
| Lĩnh vực | Ứng dụng của Tính chất chuyển tiếp |
| Toán học | Giải phương trình, chứng minh định lý |
| Khoa học máy tính | Kiểm chứng thuật toán, lý thuyết đồ thị |
| Kinh tế | Phân tích quan hệ giữa các yếu tố kinh tế |
Những ví dụ trên chỉ là một phần nhỏ của các ứng dụng của Tính chất chuyển tiếp, khẳng định tầm quan trọng của nó trong nghiên cứu và thực tiễn.
Câu hỏi thường gặp và giải đáp
Dưới đây là một số câu hỏi thường gặp về Tính chất chuyển tiếp cùng với câu trả lời chi tiết:
- Câu hỏi 1: Tính chất chuyển tiếp áp dụng cho những loại đối tượng nào trong toán học?
- Trả lời: Tính chất chuyển tiếp có thể áp dụng cho các số, biểu thức đại số, hình học, bất đẳng thức và nhiều loại đối tượng toán học khác.
- Câu hỏi 2: Làm sao để biết một quan hệ là chuyển tiếp?
- Trả lời: Một quan hệ được coi là chuyển tiếp nếu nó thỏa mãn điều kiện: nếu a liên quan đến b và b liên quan đến c, thì a cũng liên quan đến c.
- Câu hỏi 3: Tính chất chuyển tiếp có quan trọng không?
- Trả lời: Cực kỳ quan trọng. Nó là nền tảng cho rất nhiều lý thuyết và bài toán trong toán học, giúp chúng ta kết nối và so sánh các yếu tố mà không cần kiểm tra từng cặp một.
Ngoài ra, Tính chất chuyển tiếp còn giúp chúng ta hiểu và chứng minh các định lý trong toán học, là công cụ không thể thiếu trong việc xây dựng lý thuyết và giải quyết bài toán.

Tài liệu tham khảo và bài tập thực hành
Dưới đây là một số tài liệu tham khảo và bài tập thực hành để bạn có thể hiểu sâu hơn và luyện tập về Tính chất chuyển tiếp:
- Tài liệu tham khảo:
- Khan Academy: Một nguồn học trực tuyến miễn phí với các bài giảng và bài tập về Tính chất chuyển tiếp trong toán học.
- Math.net: Cung cấp định nghĩa và ví dụ cụ thể về Tính chất chuyển tiếp.
- Brilliant.org: Cung cấp các bài học sâu sắc và bài tập thực hành về nhiều khái niệm toán học, trong đó có Tính chất chuyển tiếp.
- Bài tập thực hành:
- Chứng minh rằng nếu \(a = b\), \(b = c\), và \(c = d\), thì \(a = d\) dựa trên Tính chất chuyển tiếp.
- Xác định xem các quan hệ sau có phải là chuyển tiếp không: a) "là bạn của", b) "lớn hơn hoặc bằng".
- Sử dụng Tính chất chuyển tiếp để giải bài toán: Nếu \(x + 2 = 5\) và \(5 = y + 3\), tìm giá trị của \(x\) và \(y\).
Những tài liệu và bài tập trên đây sẽ giúp bạn cải thiện kỹ năng và hiểu biết về Tính chất chuyển tiếp, một công cụ toán học cơ bản nhưng mạnh mẽ.
Hiểu và áp dụng Tính chất chuyển tiếp không chỉ mở rộng kiến thức toán học của bạn mà còn giúp giải quyết các vấn đề phức tạp một cách sáng tạo. Hãy khám phá và thực hành để làm chủ công cụ mạnh mẽ này!